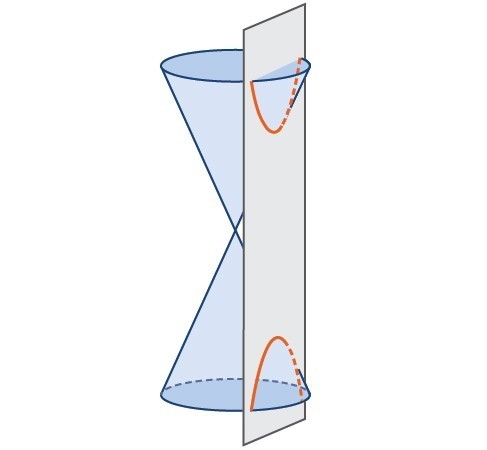
In analytic geometry a hyperbola is a conic section formed by intersecting a right circular cone with a plane at an angle such that both halves of the cone are intersected. This intersection produces two separate unbounded curves that are mirror images of each other.

A hyperbola
Like the ellipse, the hyperbola can also be defined as a set of points in the coordinate plane. A hyperbola is the set of all points [latex]\left(x,y\right)[/latex] in a plane such that the difference of the distances between [latex]\left(x,y\right)[/latex] and the foci is a positive constant. Notice that the definition of a hyperbola is very similar to that of an ellipse. The distinction is that the hyperbola is defined in terms of the difference of two distances, whereas the ellipse is defined in terms of the sum of two distances. As with the ellipse, every hyperbola has two axes of symmetry. The transverse axis is a line segment that passes through the center of the hyperbola and has vertices as its endpoints. The foci lie on the line that contains the transverse axis. The conjugate axis is perpendicular to the transverse axis and has the co-vertices as its endpoints. The center of a hyperbola is the midpoint of both the transverse and conjugate axes, where they intersect. Every hyperbola also has two asymptotes that pass through its center. As a hyperbola recedes from the center, its branches approach these asymptotes. The central rectangle of the hyperbola is centered at the origin with sides that pass through each vertex and co-vertex; it is a useful tool for graphing the hyperbola and its asymptotes. To sketch the asymptotes of the hyperbola, simply sketch and extend the diagonals of the central rectangle.
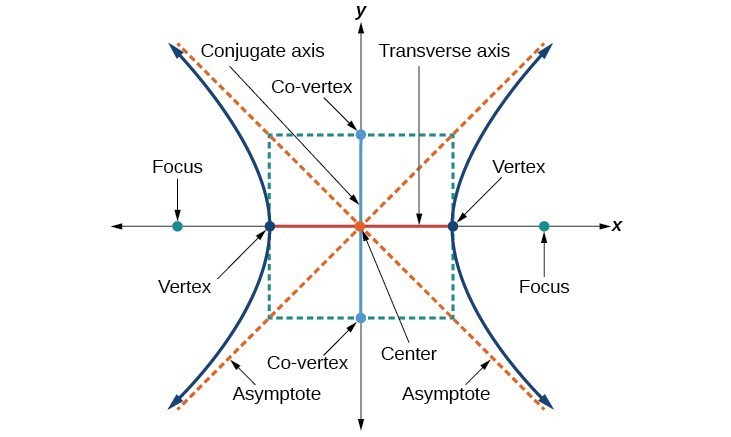
Key features of the hyperbola
In this section we will limit our discussion to hyperbolas that are positioned vertically or horizontally in the coordinate plane; the axes will either lie on or be parallel to the x- and y-axes. We will consider two cases: those that are centered at the origin, and those that are centered at a point other than the origin.
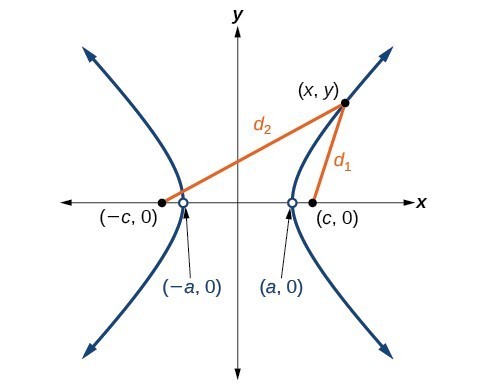
Let [latex]\left(-c,0\right)[/latex] and [latex]\left(c,0\right)[/latex] be the foci of a hyperbola centered at the origin. The hyperbola is the set of all points [latex]\left(x,y\right)[/latex] such that the difference of the distances from [latex]\left(x,y\right)[/latex] to the foci is constant. If [latex]\left(a,0\right)[/latex] is a vertex of the hyperbola, the distance from [latex]\left(-c,0\right)[/latex] to [latex]\left(a,0\right)[/latex] is [latex]a-\left(-c\right)=a+c[/latex]. The distance from [latex]\left(c,0\right)[/latex] to [latex]\left(a,0\right)[/latex] is [latex]c-a[/latex]. The difference of the distances from the foci to the vertex is
[latex]\left(a+c\right)-\left(c-a\right)=2a[/latex] If [latex]\left(x,y\right)[/latex] is a point on the hyperbola, we can define the following variables:
[latex]\begin&_=\text\left(-c,0\right)\text< to >\left(x,y\right)\\ &_=\text\left(c,0\right)\text< to >\left(x,y\right)\end[/latex] By definition of a hyperbola, [latex]\lvert_-_\rvert[/latex] is constant for any point [latex]\left(x,y\right)[/latex] on the hyperbola. We know that the difference of these distances is [latex]2a[/latex] for the vertex [latex]\left(a,0\right)[/latex]. It follows that [latex]\lvert_-_\rvert=2a[/latex] for any point on the hyperbola. The derivation of the equation of a hyperbola is based on applying the distance formula, but is again beyond the scope of this text. The standard form of an equation of a hyperbola centered at the origin with vertices [latex]\left(\pm a,0\right)[/latex] and co-vertices [latex]\left(0\pm b\right)[/latex] is [latex]\dfrac^><^>-\dfrac^>^>=1[/latex].
The standard form of the equation of a hyperbola with center [latex]\left(0,0\right)[/latex] and transverse axis on the x-axis is
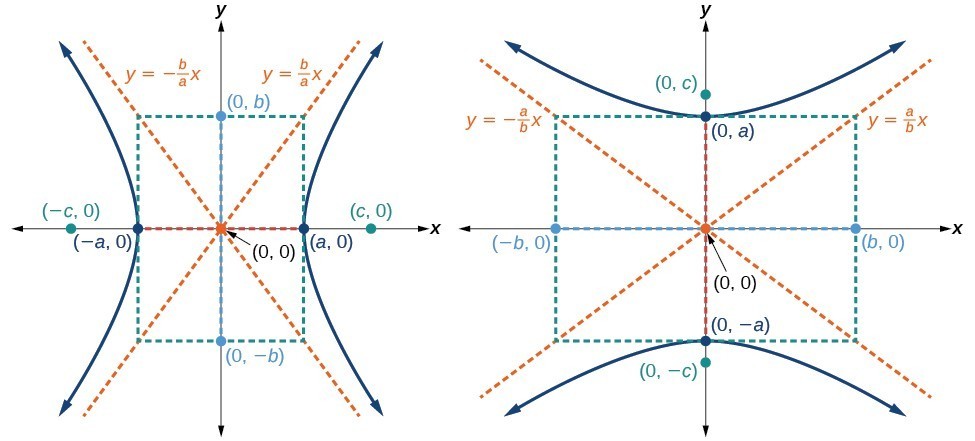
(a) Horizontal hyperbola with center [latex]\left(0,0\right)[/latex] (b) Vertical hyperbola with center [latex]\left(0,0\right)[/latex]
[latex]\begin1=\frac^>-\frac^> \\[1mm] 1=\frac^>-\frac^> \\[1mm] 1=\frac^> \\[1mm] ^=49 \\[1mm] y=\pm \sqrt=\pm 7 \end[/latex] The foci are located at [latex]\left(0,\pm c\right)[/latex]. Solving for [latex]c[/latex],
[latex]\text^=k,\textx=\pm \sqrt[/latex] Don't forget to take the plus or minus!
Just as with ellipses, writing the equation for a hyperbola in standard form allows us to calculate the key features: its center, vertices, co-vertices, foci, asymptotes, and the lengths and positions of the transverse and conjugate axes. Conversely, an equation for a hyperbola can be found given its key features. We begin by finding standard equations for hyperbolas centered at the origin. Then we will turn our attention to finding standard equations for hyperbolas centered at some point other than the origin.
What is the standard form equation of the hyperbola that has vertices [latex]\left(\pm 6,0\right)[/latex] and foci [latex]\left(\pm 2\sqrt,0\right)?[/latex]

[latex]\begin&^=^-^ \\ &^=40 - 36 && \text^\text< and >^. \\ &^=4 && \text. \end[/latex] Finally, we substitute [latex]^=36[/latex] and [latex]^=4[/latex] into the standard form of the equation, [latex]\dfrac^><^>-\dfrac^><^>=1[/latex]. The equation of the hyperbola is [latex]\dfrac^>-\dfrac^>=1[/latex].
What is the standard form equation of the hyperbola that has vertices [latex]\left(0,\pm 2\right)[/latex] and foci [latex]\left(0,\pm 2\sqrt<5>\right)?[/latex]
Like the graphs for other equations, the graph of a hyperbola can be translated. If a hyperbola is translated [latex]h[/latex] units horizontally and [latex]k[/latex] units vertically, the center of the hyperbola will be [latex]\left(h,k\right)[/latex]. This translation results in the standard form of the equation we saw previously, with [latex]x[/latex] replaced by [latex]\left(x-h\right)[/latex] and [latex]y[/latex] replaced by [latex]\left(y-k\right)[/latex].
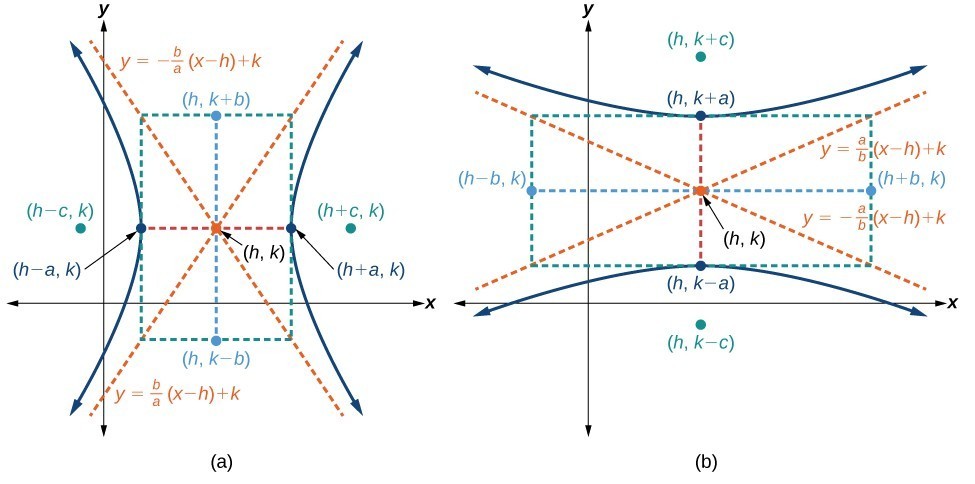
(a) Horizontal hyperbola with center [latex]\left(h,k\right)[/latex] (b) Vertical hyperbola with center [latex]\left(h,k\right)[/latex]
Like hyperbolas centered at the origin, hyperbolas centered at a point [latex]\left(h,k\right)[/latex] have vertices, co-vertices, and foci that are related by the equation [latex]
What is the standard form equation of the hyperbola that has vertices at [latex]\left(0,-2\right)[/latex] and [latex]\left(6,-2\right)[/latex] and foci at [latex]\left(-2,-2\right)[/latex] and [latex]\left(8,-2\right)?[/latex]
Answer: The y-coordinates of the vertices and foci are the same, so the transverse axis is parallel to the x-axis. Thus, the equation of the hyperbola will have the form
[latex]\beginh+c=8 \\ 3+c=8 \\ c=5 \\ ^=25 \end[/latex] Next, solve for [latex]^[/latex] using the equation [latex]^=^-^:[/latex]
What is the standard form equation of the hyperbola that has vertices [latex]\left(1,-2\right)[/latex] and [latex]\left(1,\text<8>\right)[/latex] and foci [latex]\left(1,-10\right)[/latex] and [latex]\left(1,16\right)?[/latex]
As we discussed at the beginning of this section, hyperbolas have real-world applications in many fields, such as astronomy, physics, engineering, and architecture. The design efficiency of hyperbolic cooling towers is particularly interesting. Cooling towers are used to transfer waste heat to the atmosphere and are often touted for their ability to generate power efficiently. Because of their hyperbolic form, these structures are able to withstand extreme winds while requiring less material than any other forms of their size and strength. For example a 500-foot tower can be made of a reinforced concrete shell only 6 or 8 inches wide!

Cooling towers at the Drax power station in North Yorkshire, United Kingdom (credit: Les Haines, Flickr)
The first hyperbolic towers were designed in 1914 and were 35 meters high. Today, the tallest cooling towers are in France, standing a remarkable 170 meters tall. In Example 6 we will use the design layout of a cooling tower to find a hyperbolic equation that models its sides.
The design layout of a cooling tower is shown below. The tower stands 179.6 meters tall. The diameter of the top is 72 meters. At their closest, the sides of the tower are 60 meters apart.
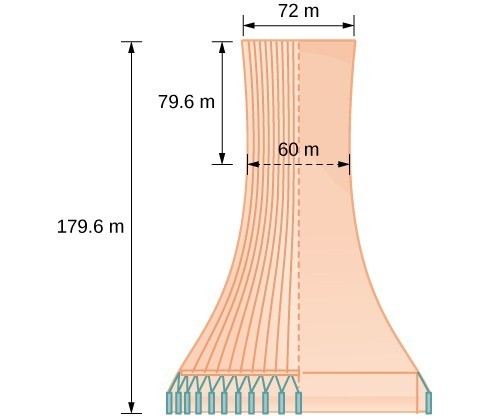
Project design for a natural draft cooling tower
Find the equation of the hyperbola that models the sides of the cooling tower. Assume that the center of the hyperbola—indicated by the intersection of dashed perpendicular lines in the figure—is the origin of the coordinate plane. Round final values to four decimal places.
Don't be discouraged if it takes several tries through the example and practice problem to understand the process. Keep trying!
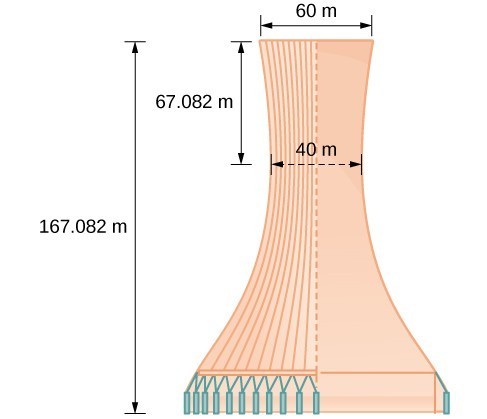
A design for a cooling tower project is shown below. Find the equation of the hyperbola that models the sides of the cooling tower. Assume that the center of the hyperbola—indicated by the intersection of dashed perpendicular lines in the figure—is the origin of the coordinate plane. Round final values to four decimal places.
Answer: The sides of the tower can be modeled by the hyperbolic equation. [latex]\dfrac^>-\dfrac^>=1\text< or >\dfrac^>^>-\dfrac^>^>=1[/latex].